Size of sub-array with max sum in C
Size of sub-array with max sum
Here, in this page we will discuss the program to find size of sub-array with max sum in C. We use Kadane’s algorithm, which runs in O(n) time.
The idea is to keep scanning through the array and calculating the maximum sub-array that ends at every position. If current sum becomes 0 then at that point we also update the starting index.
Size of sub-array with max sum in C
The size of the sub-array with the maximum sum in an array is the number of elements that are part of that sub-array.
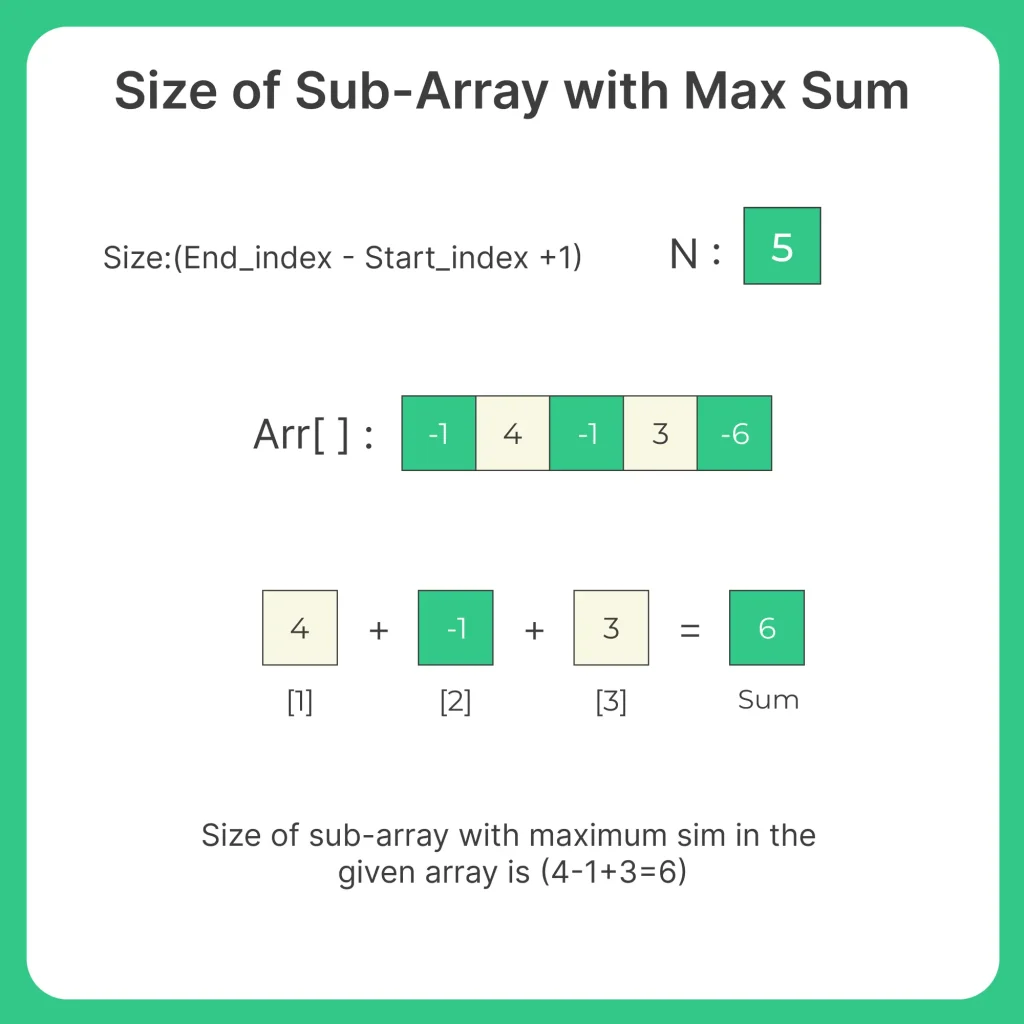
For example, in the array
[1, -2, 3, 5, -3, 2], the sub-array with the maximum sum is [3, 5], and its size is 2.
To find the size of the sub-array with the maximum sum in C, you can modify the Kadane’s algorithm implementation to keep track of the size of the sub-array as well.
Algorithm:
Create two intermediate variables max_ending_here and max_so_far .
And also two variables start and end for tracking start and the end index of the subarray with maximum sum.
Initialized these two intermediate variables using the 0.
Traverse the array from 0 to N-1 and calculate the max_ending_here and max_so_far.
Now we will keep max_so_far which indicates the maximum sum found so far.
- During the scanning of the elements from starting, and when the max_ending_here becomes 0 at that point we also update start and end variables.
C code for Size of sub-array with max sum
#include<stdio.h>
int maxSubArraySum(int a[], int size)
{
int max_so_far = 0, max_ending_here = 0,
start =0, end = 0, s=0;
for (int i=0; i< size; i++ )
{
max_ending_here += a[i];
if (max_so_far < max_ending_here)
{
max_so_far = max_ending_here;
start = s;
end = i;
}
if (max_ending_here < 0)
{
max_ending_here = 0;
s = i + 1;
}
}
return (end - start + 1);
}
int main()
{
int a[] = {-7, 3, 4, -1, -12, 1, -9, -3};
int n = sizeof(a)/sizeof(a[0]);
printf("Size of subarray with maximum sum is : %d",maxSubArraySum(a, n));
return 0;
}
Output
Size of subarray with maximum sum is : 2
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java
Login/Signup to comment