Lowest Common Ancestor in Binary Tree in C
Lowest Common Ancestor in Binary Tree
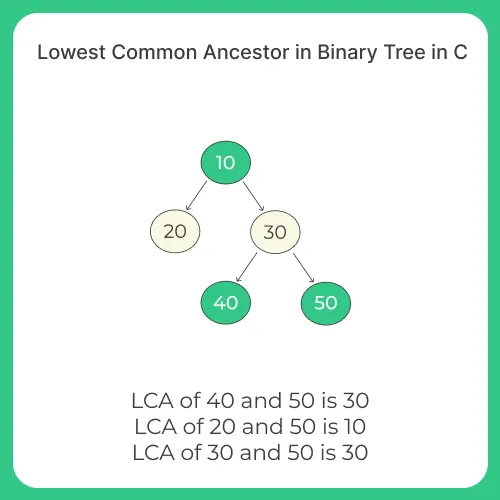
The lowest common ancestor between two nodes n1 and n2 is defined as the lowest node in T that has both n1 and n2 as descendants (where we allow a node to be a descendant of itself). Thus lca is guaranteed to exist if both the nodes are present in tree. In any other case it is NULL.
Lowest Common Ancestor in Binary Tree
Algorithm :
- Create a recursive function that takes a node and the two values n1 and n2.
- If the value of the current node is less than both n1 and n2, then LCA lies in the right subtree. Call the recursive function for the right subtree.
- If the value of the current node is greater than both n1 and n2, then LCA lies in the left subtree. Call the recursive function for the left subtree.
- If both the above cases are false then return the current node as LCA.
Code in C based on above approach
Run
#include <stdio.h>
#include <stdlib.h>
struct node
{
int data;
struct node *left, *right;
};
struct node *lca (struct node *root, int n1, int n2)
{
while (root != NULL)
{
if (root->data > n1 && root->data > n2)
root = root->left;
else if (root->data < n1 && root->data < n2)
root = root->right;
else
break;
}
return root;
}
struct node *newNode (int data)
{
struct node *node = (struct node *) malloc (sizeof (struct node));
node->data = data;
node->left = node->right = NULL;
return (node);
}
int main ()
{
struct node *root = newNode (20);
root->left = newNode (8);
root->right = newNode (22);
root->left->left = newNode (4);
root->left->right = newNode (12);
root->left->right->left = newNode (10);
root->left->right->right = newNode (14);
int n1 = 10, n2 = 14;
struct node *t = lca (root, n1, n2);
printf ("LCA of %d and %d is %d \n", n1, n2, t->data);
n1 = 14, n2 = 8;
t = lca (root, n1, n2);
printf ("LCA of %d and %d is %d \n", n1, n2, t->data);
n1 = 10, n2 = 22;
t = lca (root, n1, n2);
printf ("LCA of %d and %d is %d \n", n1, n2, t->data);
getchar ();
return 0;
}
Output:
LCA of 10 and 14 is 12 LCA of 14 and 8 is 8 LCA of 10 and 22 is 20
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java
Login/Signup to comment