Insertion in a Queue in C

March 20, 2025

Insertion in a Queue in C

How to insert an element in a Queue in C programming?

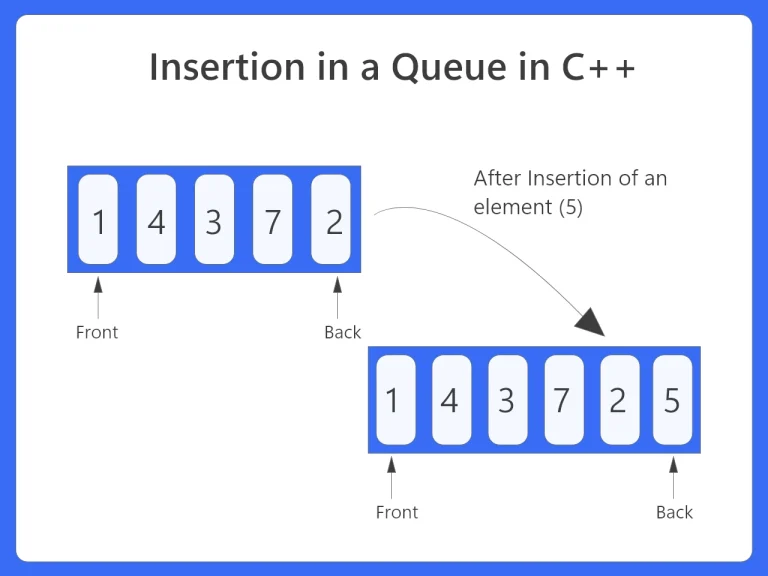
Insertion in a Queue in C is also known as enqueuing so to enqueue an element certain steps are followed which will be discussed in this article. Inserting an element in a queue is one the simplest operation that is performed on a queue which is FIFO – First in First out structure, i.e. the element added first (Enqueued) will go out of the queue first (Dequeued).

Learn more about Queue in C programming by clicking the button below:-

Step for inserting an element in a Queue in C

To insert an element in a queue that is for enqueuing we proceed using following algorithm:-
  1. Define the maximum size of queue and initialize front and rear as -1.
  2. In the main function we will initialize two variables that will store the data and the size of the queue.
  3. Accept the data that we want to enter in a queue using a for loop.
  4. After accepting the data use enqueue() function to insert the data in a queue.
  5. In this function return queue id full , if the value of rear is equal to max-1.
  6. Else increase the value of rear by 1.
  7. After this insert the data that we have accepted earlier.
  8. Now display the data of the queue using a disp() function.
  9. In this function if the value of front is equal to -1 then it means list is empty.
  10. Else initialize a for loop from front to rear and print the data that queue is holding.
Insertion in a queue in C 1

Queues In Data Structures

Deletion (Removal) in Queues Program(Dequeuing)

Reverse a Queue

Queues using Linked Lists

Implement Queue using Stack

Algorithm for enqueuing in C

As we know that Queue is a FIFO type data structure so we will be using following algorithm for insertion of an element in a Queue :-
  • IF (REAR==MAX-1)
  • RETURN QUEUE FULL
  • ELSE
  • REAR+REAR+1
  • QUEUE[REAR]=DATA
  • IF(FRONT== -1)
  • FRONT = 0

Code for inserting an element in a queue in C (Enqueuing)

Run 
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>

#define MAX 6

int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;

int peek ()
{
  return intArray[front];
}

bool isEmpty ()
{
  return itemCount == 0;
}

bool isFull ()
{
  return itemCount == MAX;
}

int size ()
{
  return itemCount;
}

void enqueue(int data)
{

  if (!isFull ())
    {

      if (rear == MAX - 1)
	{
	  rear = -1;
	}

      intArray[++rear] = data;
      itemCount++;
    }
}

int dequeue()
{
  int data = intArray[front++];

  if (front == MAX)
    {
      front = 0;
    }

  itemCount--;
  return data;
}

int main ()
{

  enqueue (3);
  enqueue (5);
  enqueue (9);
  enqueue (1);
  enqueue (12);
  enqueue (15);

  if (isFull ())
    {
      printf ("Queue is full!\n");
    }

  int num = dequeue ();

  printf ("Element removed: %d\n", num);

  enqueue (16);
  enqueue (17);
  enqueue (18);

  printf ("Element at front: %d\n", peek ());

  printf ("----------------------\n");
  printf ("index : 5 4 3 2  1  0\n");
  printf ("----------------------\n");
  printf ("Queue:  ");

  while (!isEmpty ())
    {
      int n = dequeue();
      printf ("%d ", n);
    }
}

Output

Queue is full!
Element removed: 3
Element at front: 5
----------------------
index : 5 4 3 2 1 0
----------------------
Queue: 5 9 1 12 15 16