Edit Distance
Edit Distance
In the edit distance problem, we have to find the minimum number of operations required to convert one string to another. It is a very famous interview problem asked many times in coding interviews as well as in coding rounds. In this article, we provide a c++ solution with an explanation of the problem.

Edit Distance Problem Description
We are given two strings A and B. We have to perform minimum number of operations on A to convert it to string B. The allowed operations are –
- Insert a character.
- Replace a character by any other character.
- Delete a character.
Input:
- First line contains string A.
- Second line contains string B.
Output:
The minimum number of operations.
Edit Distance Problem Solution Explanation
Solution (Top Down):
To build a top down solution we must follow the following steps –
- Break Down the Problem – The problem can be break down as follows. Consider a function F(i,j) that returns the minimum number of operations required to convert A[0…i] to B[0…j]. There are two options –
if(A[i]==B[j])
F(i,j) = F(i-1,j-1) // No operation is needed
else
Option 1 =1+ F(i,j-1) // Insert B[j] in A
Option 2 =1+ F(i-1,j) // Remove A[i]
Option 3 = 1 + F(i-1,j-1) // Replace A[i] with B[j]
Now we simply return minimum of all these options.
- Find the base case – The base case in this problem is quite simple. It is when we have no characters left in any one string.
- Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. The optimal substructure and overlapping sub problems properties can be visualized below.
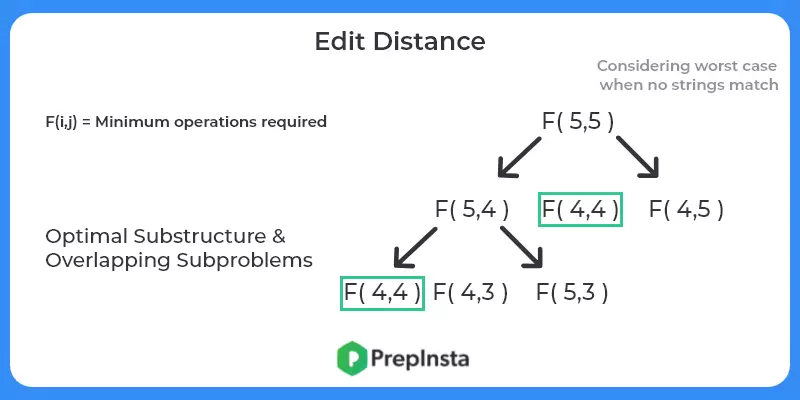
Bottom up Solution
In previous solution we call the function f(n-1,m-1) {n length of first string, m length of second string}.
Here instead of breaking problem into smaller problems we first solve smaller problems and iteratively use them to solve bigger problems.
Code
Output
Top Down Answer 8
Bottom Up Answer 8




Login/Signup to comment