Cutting a Rod

November 6, 2021

Cutting a Rod

In the Cutting a Rod problem we are given a large rod. We have to cut the rod into smaller pieces to maximize the price. In this article, we provide C++ code with an explanation of the problem.

Cutting a Rod problem Description

Cutting a Rod Problem Description

In this problem we are given a rod of size n. We are also given the selling price of smaller rods each of size 1 to n. We have to make multiple cuts on the larger rod in order to maximize the selling price.

Input:

  • First line contains integer n – The size of rod.
  • Second line contains n integers – Selling prices of rods of length 1 to n.

Output:

  • The maximum price achievable.

Cutting a Rod Solution

Memoization or Top Down Solution

To build a top-down solution we must follow the following steps –

  • Break Down the Problem – In this step, we try to break down the problem into smaller problems and assume recursion will solve the smaller problems.

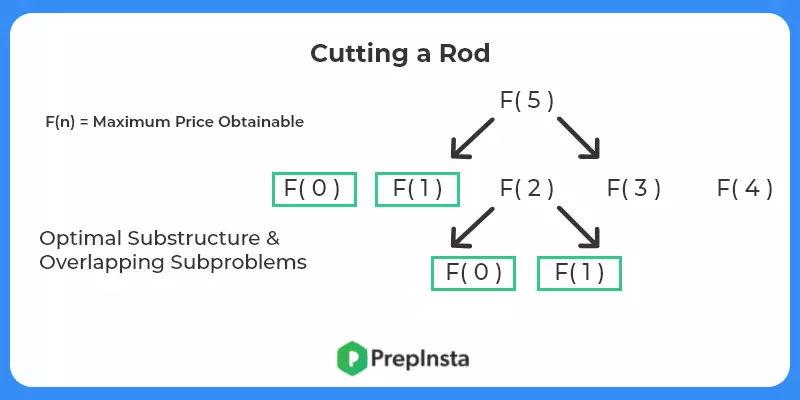
F(N) = Max price achievable for a rod of length N.

F(N) = max( F(N-i)+cost[i]) { i belongs to 1 to N}

  • Find the base case – The base case is the smallest known solution. Here it is when the length is 0 we return 0 cost.
  • Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. The optimal substructure and overlapping sub problems properties can be visualized below.
Cutting a Rod memoization

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 10005;
int memo[N];
int f(int cost[], int n)
{
    if (n <= 0)
        return 0;
    if (memo[n] != –1)
        return memo[n];
    int ans = INT_MIN;
    for (int cut = 1; cut <= n; cut++)
    {
        int cur = cost[cut – 1] + f(cost, n – cut);
        ans = max(ans, cur);
    }
    return memo[n] = ans;
}
int main()
{
    memset(memo, –1, sizeof memo);
    int n = 5;
    int arr[n] = {1, 2, 3, 2, 1};
    cout << “Maximum Cost is “ << f(arr, n) << endl;
    return 0;
}

Output

Maximum Cost is 5

Bottom up Solution

Here we create a dp array of length n+1. We find the maximum price for each length starting from length = 1 to length = n.

Code

#include <bits/stdc++.h>
using namespace std;
int f(int cost[], int n)
{
    int dp[n + 1];
    dp[0] = 0;

    for (int length = 1; length <= n; length++)
    {
        dp[length] = INT_MIN;
        for (int cut = 1; cut <= length; cut++)
        {
            dp[length] = max(dp[length], cost[cut – 1] + dp[length – cut]);
        }
    }

    return dp[n];
}

int main()
{
    int n = 5;
    int arr[n] = {1, 2, 3, 2, 1};
    cout << “Maximum Cost is “ << f(arr, n) << endl;
    return 0;
}

Output

Maximum Cost is 5