Java Program for Trapping Rain water problem
Trapping Rain Water in Java
Here, in this page we will discuss one of the famous problem of Trapping Rain Water in Java. We are given with n non-negative integers representing an elevation map where the width of each bar is 1, we need to compute how much water it is able to trap after raining.
Example :
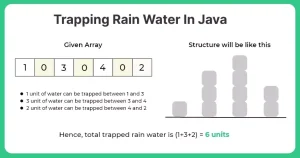
- Input : arr[5] = {3, 0, 2, 0, 4}
- Output : 7
- Explanation : We can trap “3 units” of water between 3 and 2, “1 unit” on top of bar 2 and “3 units” between 2 and 4. See below diagram also.

Method 1
- Take the size of the array from the user and store it in variable say n.
- Take n integers from the user and store them in an array say arr[].
- Now, iterate the entire array,
- For every i-th element, traverse the array from 0 to i and find the maximum height (a) and after that traverse the array from the i index to n, and find the maximum height (b).
- The amount of water that will be stored in this column is min(a, b) – arr[i], add this value to the total amount of water stored.
- After complete iteration print the amount of water.
Code for Trapping Rain Water in Java
Run
public
class Main {
public
static int maxWater(int[] arr, int n) {
// To store the maximum water
// that can be stored
int res = 0;
// For every element of the array
// except first and last element
for (int i = 1; i < n - 1; i++) {
// Find maximum element on its left
int left = arr[i];
for (int j = 0; j < i; j++) {
left = Math.max(left, arr[j]);
}
// Find maximum element on its right
int right = arr[i];
for (int j = i + 1; j < n; j++) {
right = Math.max(right, arr[j]);
}
// Update maximum water value
res += Math.min(left, right) - arr[i];
}
return res;
}
// Driver code
public
static void main(String[] args) {
int[] arr = {0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
int n = arr.length;
System.out.print(maxWater(arr, n));
}
}
6
Time and Space complexity
Time-Complexity : O(n^2)
Space-Complexity : O(1)
Method 2
- Now, Create two array say left[] and right[] of size n.
- Create a variable say max_ and set its value to INT_MIN.
- Run one loop from 0 to n and in each iteration update max_ as max_ = max(max_, arr[i]) and also assign left[i] = max_.
- Again, update max_ = INT_MIN.
- Run another loop from n-1 to 0 and in each iteration update max_ as max_ = max(max_, arr[i]) and also assign right[i] = max_.
- Now, traverse the array from 0 to n,
- The amount of water that will be stored in this column is min(a,b) – array[i],(where a = left[i] and b = right[i]) add this value to total amount of water stored
- After complete iteration print the amount of water.
Code for Trapping Rain Water in Java
Run
public class Main {
static int findWater(int arr[], int n) {
// initialize output
int result = 0;
// maximum element on left and right
int left_max = 0, right_max = 0;
// indices to traverse the array
int lo = 0, hi = n - 1;
while (lo <= hi) {
if (arr[lo] < arr[hi]) {
if (arr[lo] > left_max)
// update max in left
left_max = arr[lo];
else
// water on curr element =
// max - curr
result += left_max - arr[lo];
lo++;
}
else
{
if (arr[hi] > right_max)
// update right maximum
right_max = arr[hi];
else
result += right_max - arr[hi];
hi--;
}
}
return result;
}
/* Driver program to test above function */
public
static void main(String[] args) {
int arr[] = {0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
int n = arr.length;
System.out.println("Maximum water that " + "can be accumulated is " + findWater(arr, n));
}
}
Maximum water that can be accumulated is 6
This is an Alert
Time Complexity: O(n)
Only one traversal of the array is needed.
Auxiliary Space: O(1).
As no extra space is required
Method 3
Instead of maintaining two arrays of size n for storing the left and a right max of each i-th element, we can maintain two variables to store the maximum till that point. Since water trapped at any element = min(max_left, max_right) – arr[i]. We calculate water trapped on smaller elements out of arr[lo] and arr[hi] first and move the pointers till lo doesn’t cross hi.
Code for Trapping Rain Water in Java
Run
public class Main {
static int arr[] = new int[]{0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
// Method for maximum amount of water
static int findWater(int n) {
int left[] = new int[n];
int right[] = new int[n];
// Initialize result
int water = 0;
// Fill left array
left[0] = arr[0];
for (int i = 1; i < n; i++) left[i] = Math.max(left[i - 1], arr[i]);
// Fill right array
right[n - 1] = arr[n - 1];
for (int i = n - 2; i >= 0; i--) right[i] = Math.max(right[i + 1], arr[i]);
for (int i = 0; i < n; i++) water += Math.min(left[i], right[i]) - arr[i];
return water;
}
// Driver method to test the above function
public
static void main(String[] args) {
System.out.println("Maximum water that can be accumulated is " + findWater(arr.length));
}
}
Maximum water that can be accumulated is 6
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription



Login/Signup to comment