Lowest Common Ancestor in Binary Tree in C
Lowest Common Ancestor in Binary Tree
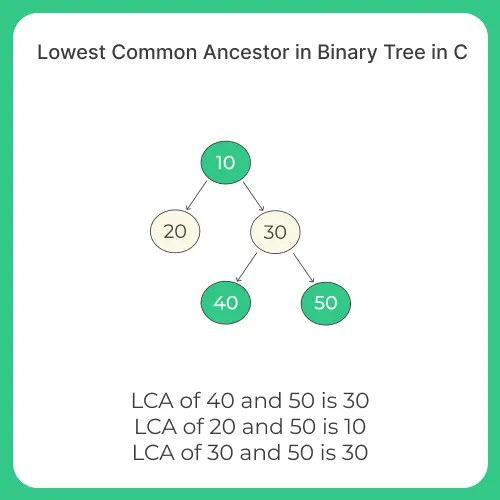
The lowest common ancestor between two nodes n1 and n2 is defined as the lowest node in T that has both n1 and n2 as descendants (where we allow a node to be a descendant of itself). Thus lca is guaranteed to exist if both the nodes are present in tree. In any other case it is NULL.
Lowest Common Ancestor in Binary Tree
Algorithm :
- Create a recursive function that takes a node and the two values n1 and n2.
- If the value of the current node is less than both n1 and n2, then LCA lies in the right subtree. Call the recursive function for the right subtree.
- If the value of the current node is greater than both n1 and n2, then LCA lies in the left subtree. Call the recursive function for the left subtree.
- If both the above cases are false then return the current node as LCA.
Code in C based on above approach
Run
#include <stdio.h>
#include <stdlib.h>
struct node
{
int data;
struct node *left, *right;
};
struct node *lca (struct node *root, int n1, int n2)
{
while (root != NULL)
{
if (root->data > n1 && root->data > n2)
root = root->left;
else if (root->data < n1 && root->data < n2)
root = root->right;
else
break;
}
return root;
}
struct node *newNode (int data)
{
struct node *node = (struct node *) malloc (sizeof (struct node));
node->data = data;
node->left = node->right = NULL;
return (node);
}
int main ()
{
struct node *root = newNode (20);
root->left = newNode (8);
root->right = newNode (22);
root->left->left = newNode (4);
root->left->right = newNode (12);
root->left->right->left = newNode (10);
root->left->right->right = newNode (14);
int n1 = 10, n2 = 14;
struct node *t = lca (root, n1, n2);
printf ("LCA of %d and %d is %d \n", n1, n2, t->data);
n1 = 14, n2 = 8;
t = lca (root, n1, n2);
printf ("LCA of %d and %d is %d \n", n1, n2, t->data);
n1 = 10, n2 = 22;
t = lca (root, n1, n2);
printf ("LCA of %d and %d is %d \n", n1, n2, t->data);
getchar ();
return 0;
}
Output:
LCA of 10 and 14 is 12 LCA of 14 and 8 is 8 LCA of 10 and 22 is 20



Login/Signup to comment