Subtree of Another Tree
Subtree of Another Tree – Easy Level Problem
Given the roots of two binary trees, root and subRoot, return true if subRoot is a subtree of root, otherwise return false.
A subtree of a binary tree is a tree consisting of a node in the binary tree and all its descendants. The binary tree itself is also considered its own subtree.
Example 1:
Illustration 1:
Input: root = [1,2,3,4,5], subRoot = [2,4,5]
Output: true
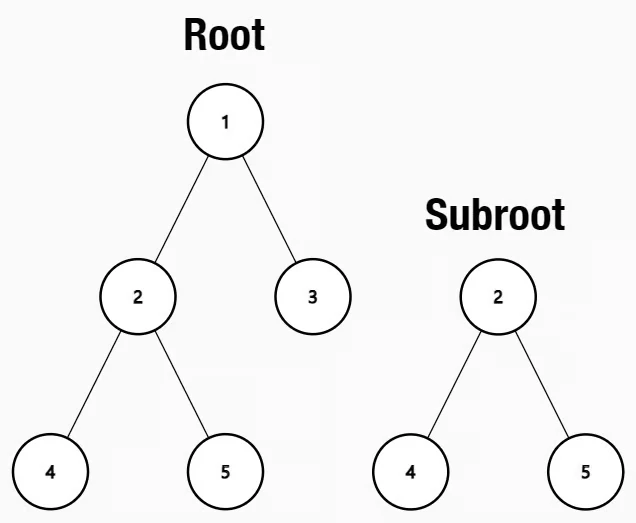
Output: true
Example 2:
Illustration 2:
Input: root = [1,2,3,4,5,null,null,6], subRoot = [2,4,5]
Output: false
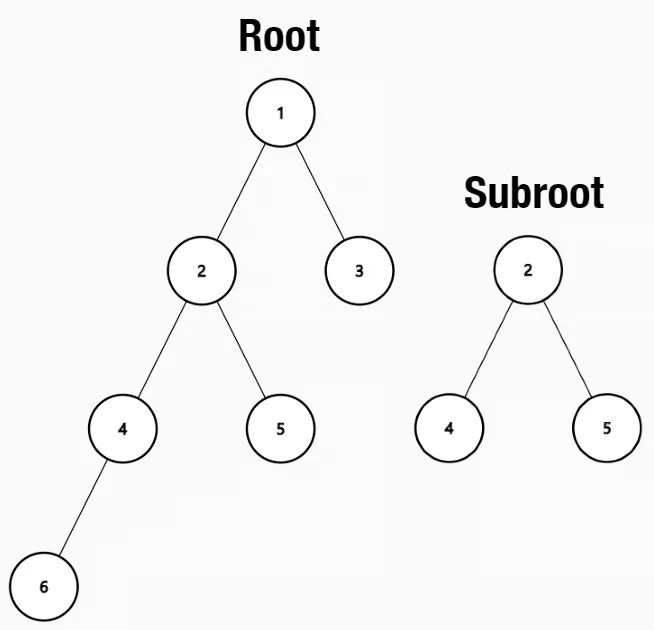
Output: false
Constraints:
- 0 <= The number of nodes in both trees <= 100.
- -100 <= root.val, subRoot.val <= 100
Hints to Solve Subtree of Another Tree
Recommendation for Time and Space Complexity:
Aim for a solution with a time complexity of O(m x n) or better and a space complexity of O(m + n).
Where, m and n, number of nodes in roots and subroots.
Hint 1 :
- Subtree of a tree is a smaller tree rooted at a specific node of the larger tree.
- To check if subRoot matches any subtree of root, think about using recursion.
- You can use the approach where you check if two trees are identical in structure and values.
Hint 2 :
- Two trees are identical when they have the same structure and all corresponding nodes have the same values.
- Use Depth First Search (DFS) to solve this problem by comparing the trees node by node. How would you implement this in code?
Hint 3 :
- Traverse the root tree, and for each node, check if the subtree starting at that node matches subRoot.
- Use a helper function, sameTree(root1, root2), to verify if the two trees are identical in structure and node values.
There are mainly 2 approach to solve this problem:
- Depth First Search (DFS)
- Serialization And Pattern Matching
1. Depth First Search (DFS) Method
Traverse the main tree (root) using DFS, and at each node, check if the subtree starting from that node matches subRoot. Use a helper function to compare the structure and values of the two trees recursively.
- Time complexity: O(m x n)
- Space complexity: O(m + n)
Where m is the number of nodes in subRoot and n is the number of nodes in root.
Code
C++
Java
Python
JavaScript
C++
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
if (!subRoot) {
return true;
}
if (!root) {
return false;
}
if (sameTree(root, subRoot)) {
return true;
}
return isSubtree(root->left, subRoot) ||
isSubtree(root->right, subRoot);
}
bool sameTree(TreeNode* root, TreeNode* subRoot) {
if (!root && !subRoot) {
return true;
}
if (root && subRoot && root->val == subRoot->val) {
return sameTree(root->left, subRoot->left) &&
sameTree(root->right, subRoot->right);
}
return false;
}
};
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if (subRoot == null) {
return true;
}
if (root == null) {
return false;
}
if (sameTree(root, subRoot)) {
return true;
}
return isSubtree(root.left, subRoot) ||
isSubtree(root.right, subRoot);
}
public boolean sameTree(TreeNode root, TreeNode subRoot) {
if (root == null && subRoot == null) {
return true;
}
if (root != null && subRoot != null && root.val == subRoot.val) {
return sameTree(root.left, subRoot.left) &&
sameTree(root.right, subRoot.right);
}
return false;
}
}
Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
if not subRoot:
return True
if not root:
return False
if self.sameTree(root, subRoot):
return True
return (self.isSubtree(root.left, subRoot) or
self.isSubtree(root.right, subRoot))
def sameTree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
if not root and not subRoot:
return True
if root and subRoot and root.val == subRoot.val:
return (self.sameTree(root.left, subRoot.left) and
self.sameTree(root.right, subRoot.right))
return False
JavaScript
/**
* Definition for a binary tree node.
* class TreeNode {
* constructor(val = 0, left = null, right = null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* @param {TreeNode} root
* @param {TreeNode} subRoot
* @return {boolean}
*/
isSubtree(root, subRoot) {
if (!subRoot) {
return true;
}
if (!root) {
return false;
}
if (this.sameTree(root, subRoot)) {
return true;
}
return (
this.isSubtree(root.left, subRoot) ||
this.isSubtree(root.right, subRoot)
);
}
/**
* @param {TreeNode} root
* @param {TreeNode} subRoot
* @return {boolean}
*/
sameTree(root, subRoot) {
if (!root && !subRoot) {
return true;
}
if (root && subRoot && root.val === subRoot.val) {
return (
this.sameTree(root.left, subRoot.left) &&
this.sameTree(root.right, subRoot.right)
);
}
return false;
}
}
2. Serialization And Pattern Matching Method
Serialize both trees into strings, where each tree is represented as a unique sequence of node values and structure. Use pattern matching to check if the serialized subRoot appears as a substring in the serialized root.
- Time complexity: O(m + n)
- Space complexity: O(m + n)
Code
C++
Java
Python
JavaScript
C++
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
string serialize(TreeNode* root) {
if (root == nullptr) {
return "$#";
}
return "$" + to_string(root->val) +
serialize(root->left) + serialize(root->right);
}
vector z_function(string s) {
vector z(s.length());
int l = 0, r = 0, n = s.length();
for (int i = 1; i < n; i++) {
if (i <= r) {
z[i] = min(r - i + 1, z[i - l]);
}
while (i + z[i] < n && s[z[i]] == s[i + z[i]]) {
z[i]++;
}
if (i + z[i] - 1 > r) {
l = i;
r = i + z[i] - 1;
}
}
return z;
}
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
string serialized_root = serialize(root);
string serialized_subRoot = serialize(subRoot);
string combined = serialized_subRoot + "|" + serialized_root;
vector z_values = z_function(combined);
int sub_len = serialized_subRoot.length();
for (int i = sub_len + 1; i < combined.length(); i++) {
if (z_values[i] == sub_len) {
return true;
}
}
return false;
}
};
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class Solution {
public String serialize(TreeNode root) {
if (root == null) {
return "$#";
}
return "$" + root.val + serialize(root.left) + serialize(root.right);
}
public int[] z_function(String s) {
int[] z = new int[s.length()];
int l = 0, r = 0, n = s.length();
for (int i = 1; i < n; i++) {
if (i <= r) {
z[i] = Math.min(r - i + 1, z[i - l]);
}
while (i + z[i] < n && s.charAt(z[i]) == s.charAt(i + z[i])) {
z[i]++;
}
if (i + z[i] - 1 > r) {
l = i;
r = i + z[i] - 1;
}
}
return z;
}
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
String serialized_root = serialize(root);
String serialized_subRoot = serialize(subRoot);
String combined = serialized_subRoot + "|" + serialized_root;
int[] z_values = z_function(combined);
int sub_len = serialized_subRoot.length();
for (int i = sub_len + 1; i < combined.length(); i++) {
if (z_values[i] == sub_len) {
return true;
}
}
return false;
}
}
Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def serialize(self, root: Optional[TreeNode]) -> str:
if root == None:
return "$#"
return ("$" + str(root.val) +
self.serialize(root.left) + self.serialize(root.right))
def z_function(self, s: str) -> list:
z = [0] * len(s)
l, r, n = 0, 0, len(s)
for i in range(1, n):
if i <= r:
z[i] = min(r - i + 1, z[i - l])
while i + z[i] < n and s[z[i]] == s[i + z[i]]:
z[i] += 1
if i + z[i] - 1 > r:
l, r = i, i + z[i] - 1
return z
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
serialized_root = self.serialize(root)
serialized_subRoot = self.serialize(subRoot)
combined = serialized_subRoot + "|" + serialized_root
z_values = self.z_function(combined)
sub_len = len(serialized_subRoot)
for i in range(sub_len + 1, len(combined)):
if z_values[i] == sub_len:
return True
return False
JavaScript
/**
* Definition for a binary tree node.
* class TreeNode {
* constructor(val = 0, left = null, right = null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* @param {TreeNode} root
* @return {string}
*/
serialize(root) {
if (root === null) {
return "$#";
}
return "$" + root.val +
this.serialize(root.left) + this.serialize(root.right);
}
/**
* @param {string} s
* @return {number[]}
*/
z_function(s) {
const z = new Array(s.length).fill(0);
let l = 0, r = 0, n = s.length;
for (let i = 1; i < n; i++) {
if (i <= r) {
z[i] = Math.min(r - i + 1, z[i - l]);
}
while (i + z[i] < n && s[z[i]] === s[i + z[i]]) {
z[i]++;
}
if (i + z[i] - 1 > r) {
l = i;
r = i + z[i] - 1;
}
}
return z;
}
/**
* @param {TreeNode} root
* @param {TreeNode} subRoot
* @return {boolean}
*/
isSubtree(root, subRoot) {
const serialized_root = this.serialize(root);
const serialized_subRoot = this.serialize(subRoot);
const combined = serialized_subRoot + "|" + serialized_root;
const z_values = this.z_function(combined);
const sub_len = serialized_subRoot.length;
for (let i = sub_len + 1; i < combined.length; i++) {
if (z_values[i] === sub_len) {
return true;
}
}
return false;
}
}
3. Breadth First Search Method
The BFS method uses a queue to traverse the tree level by level. Nodes at the same depth are processed together. By counting the levels traversed, you determine the maximum depth of the tree. This approach is efficient for level-order traversal.
- Time complexity: O(n)
- Space complexity: O(n)
Code
C++
Java
Python
JavaScript
C++
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
queue<TreeNode*> q;
if (root != nullptr) {
q.push(root);
}
int level = 0;
while (!q.empty()) {
int size = q.size();
for (int i = 0; i < size; i++) { TreeNode* node = q.front(); q.pop(); if (node->left != nullptr) {
q.push(node->left);
}
if (node->right != nullptr) {
q.push(node->right);
}
}
level++;
}
return level;
}
};
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class Solution {
public int maxDepth(TreeNode root) {
Queue<TreeNode> q = new LinkedList<>();
if (root != null) {
q.add(root);
}
int level = 0;
while (!q.isEmpty()) {
int size = q.size();
for (int i = 0; i < size; i++) {
TreeNode node = q.poll();
if (node.left != null) {
q.add(node.left);
}
if (node.right != null) {
q.add(node.right);
}
}
level++;
}
return level;
}
}
Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
q = deque()
if root:
q.append(root)
level = 0
while q:
for i in range(len(q)):
node = q.popleft()
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
level += 1
return level
JavaScript
/**
* Definition for a binary tree node.
* class TreeNode {
* constructor(val = 0, left = null, right = null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* @param {TreeNode} root
* @return {number}
*/
maxDepth(root) {
const q = new Queue();
if (root !== null) {
q.push(root);
}
let level = 0;
while (q.size() > 0) {
const size = q.size();
for (let i = 0; i < size; i++) {
const node = q.pop();
if (node.left !== null) {
q.push(node.left);
}
if (node.right !== null) {
q.push(node.right);
}
}
level++;
}
return level;
}
}
