Maximum Depth of Binary Tree
Maximum Depth of Binary Tree – Medium Level Problem
You are given the root of a binary tree, and your task is to determine its depth.
Depth of a binary tree refers to the number of nodes present along the longest path starting from the root node down to the farthest leaf node.
In simpler terms, it measures how deep the tree goes from the topmost node (the root) to the bottommost node (a leaf with no children). This depth represents the maximum number of steps needed to traverse the tree vertically.

Example 1
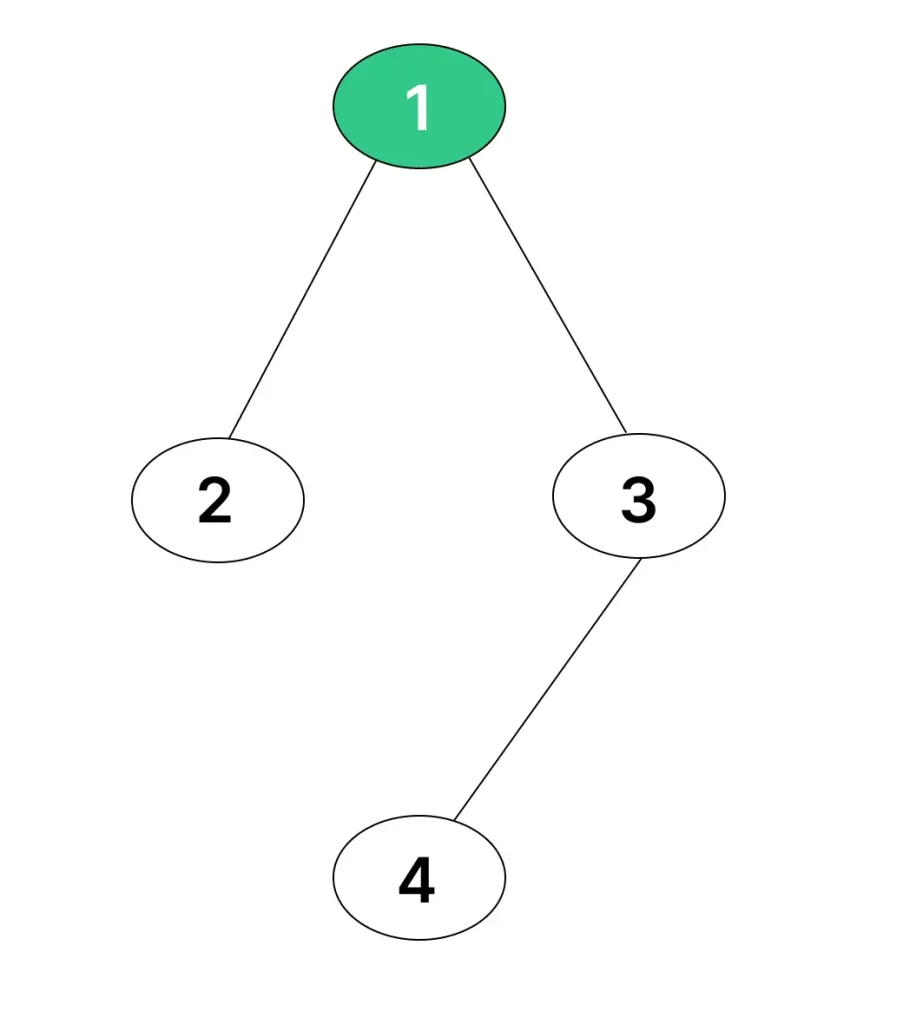
Output: 3
Output: 0
Constraints:
- 0 <= The number of nodes in the tree <= 100.
- -100 <= Node.val <= 100
Maximum Depth of Binary Tree
Recommendation for Time and Space Complexity – You should aim for a solution with O(n) time and O(n) space, where n is the number of nodes in the tree.
Hints for solving problems
Hint 1 :
From the definition of binary tree’s maximum depth, Can you think of a way to achieve this recursively? Maybe you should consider the max depth of the subtrees first before computing the maxdepth at the root.
Hint 2 :
We use the Depth First Search (DFS) algorithm to find the maximum depth of a binary tree, starting from the root. For the subtrees rooted at the left and right children of the root node, we calculate their maximum depths recursively going through left and right subtrees. We return 1 + max(leftDepth, rightDepth). Why?
There are mainly 3 approach to solve this problem-
- Recursive DFS Method
- Iterative DFS(Stack) Method
- Breadth First Search Method
1. Recursive DFS Method
In this approach, you use recursion to traverse the tree. At each node, the function is called recursively for the left and right children to calculate their depths. The maximum of these depths is taken, and 1 is added to account for the current node. This method is simple and intuitive for tree traversal.
- Time complexity: O(n)
- Space complexity: O(h)
- Best Case (balanced tree): O(log(n))
- Worst Case (degenerate tree): O(n)
Where n is the number of nodes in the tree and h is the height of the tree.
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == nullptr) {
return 0;
}
return 1 + max(maxDepth(root->left), maxDepth(root->right));
}
};
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
}
}
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))
/**
* Definition for a binary tree node.
* class TreeNode {
* constructor(val = 0, left = null, right = null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* @param {TreeNode} root
* @return {number}
*/
maxDepth(root) {
if (root === null) {
return 0;
}
return (
1 + Math.max(this.maxDepth(root.left), this.maxDepth(root.right))
);
}
}
2. Iterative DFS(Stack) Method
This method uses a stack to simulate the depth-first traversal iteratively. Each node is paired with its depth and pushed onto the stack. As you process each node, you update the maximum depth by comparing the current depth of the node with the recorded value.
- Time complexity: O(n)
- Space complexity: O(n)
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
stack> stack;
stack.push({root, 1});
int res = 0;
while (!stack.empty()) {
pair current = stack.top();
stack.pop();
TreeNode* node = current.first;
int depth = current.second;
if (node != nullptr) {
res = max(res, depth);
stack.push({node->left, depth + 1});
stack.push({node->right, depth + 1});
}
}
return res;
}
};
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class Solution {
public int maxDepth(TreeNode root) {
Stack> stack = new Stack<>();
stack.push(new Pair<>(root, 1));
int res = 0;
while (!stack.isEmpty()) {
Pair current = stack.pop();
TreeNode node = current.getKey();
int depth = current.getValue();
if (node != null) {
res = Math.max(res, depth);
stack.push(new Pair<>(node.left, depth + 1));
stack.push(new Pair<>(node.right, depth + 1));
}
}
return res;
}
}
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
stack = [[root, 1]]
res = 0
while stack:
node, depth = stack.pop()
if node:
res = max(res, depth)
stack.append([node.left, depth + 1])
stack.append([node.right, depth + 1])
return res
/**
* Definition for a binary tree node.
* class TreeNode {
* constructor(val = 0, left = null, right = null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* @param {TreeNode} root
* @return {number}
*/
maxDepth(root) {
const stack = [[root, 1]];
let res = 0;
while (stack.length > 0) {
const current = stack.pop();
const node = current[0];
const depth = current[1];
if (node !== null) {
res = Math.max(res, depth);
stack.push([node.left, depth + 1]);
stack.push([node.right, depth + 1]);
}
}
return res;
}
}
3. Breadth First Search Method
The BFS method uses a queue to traverse the tree level by level. Nodes at the same depth are processed together. By counting the levels traversed, you determine the maximum depth of the tree. This approach is efficient for level-order traversal.
- Time complexity: O(n)
- Space complexity: O(n)
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
queue<TreeNode*> q;
if (root != nullptr) {
q.push(root);
}
int level = 0;
while (!q.empty()) {
int size = q.size();
for (int i = 0; i < size; i++) { TreeNode* node = q.front(); q.pop(); if (node->left != nullptr) {
q.push(node->left);
}
if (node->right != nullptr) {
q.push(node->right);
}
}
level++;
}
return level;
}
};
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class Solution {
public int maxDepth(TreeNode root) {
Queue<TreeNode> q = new LinkedList<>();
if (root != null) {
q.add(root);
}
int level = 0;
while (!q.isEmpty()) {
int size = q.size();
for (int i = 0; i < size; i++) {
TreeNode node = q.poll();
if (node.left != null) {
q.add(node.left);
}
if (node.right != null) {
q.add(node.right);
}
}
level++;
}
return level;
}
}
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
q = deque()
if root:
q.append(root)
level = 0
while q:
for i in range(len(q)):
node = q.popleft()
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
level += 1
return level
/**
* Definition for a binary tree node.
* class TreeNode {
* constructor(val = 0, left = null, right = null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* @param {TreeNode} root
* @return {number}
*/
maxDepth(root) {
const q = new Queue();
if (root !== null) {
q.push(root);
}
let level = 0;
while (q.size() > 0) {
const size = q.size();
for (let i = 0; i < size; i++) {
const node = q.pop();
if (node.left !== null) {
q.push(node.left);
}
if (node.right !== null) {
q.push(node.right);
}
}
level++;
}
return level;
}
}


