Balanced Binary Tree Problem
Checking for Balanced Binary Tree or Not
You are given a binary tree, and your goal is to determine whether it is height-balanced or not. Return true if the tree is height-balanced and false otherwise.
Binary tree is said to be height-balanced if the difference in height between the left and right subtrees of every node in the tree is no more than 1. This means that for each node, the tree does not lean too heavily to one side.
To check this, you must calculate the height of the left and right subtrees for each node and ensure the difference is 0 or 1 for all nodes throughout the tree. If any node fails this condition, the tree is not height-balanced.
Example 1
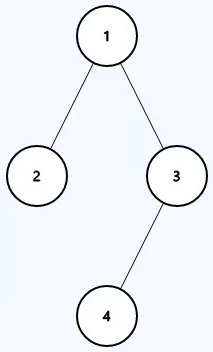
Output: true
Example 2
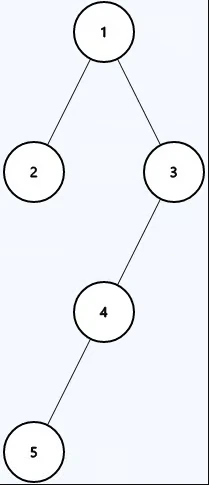
Output: false
Output: true
Constraints:
- The number of nodes in the tree is in the range [0, 1000].
- -1000 <= Node.val <= 1000
Maximum Depth of Binary Tree
Recommendation for Time and Space Complexity – You should aim for a solution with O(n) time and O(n) space, where n is the number of nodes in the tree.
Hints for solving problems
Hint 1 :
A brute force solution would involve traversing every node and checking whether the tree rooted at each node is balanced by computing the heights of its left and right subtrees. This approach would result in an O(n^2) solution. Can you think of a more efficient way? Perhaps you could avoid repeatedly computing the heights for every node by determining balance and height in a single traversal.
Hint 2 :
We can use the Depth First Search (DFS) algorithm to compute the heights at each node. While calculating the heights of the left and right subtrees, we also check if the tree rooted at the current node is balanced. If leftHeight – rightHeight > 1, we update a global variable, such as isBalanced = False. After traversing all the nodes, the value of isBalanced indicates whether the entire tree is balanced or not.
There are mainly 3 approach to solve this problem-
- Brute Force Method
- Depth First Search Method
- Depth First Search(Stack) Method
1. Brute Force Method
In this approach, we find the height of the left and right subtrees for every node and check if the difference is more than 1. If it is, the tree is not balanced. While easy to understand, this method is slow because it repeatedly calculates the height, making it less efficient.
- Time complexity: O(n^2)
- Space complexity: O(n)
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isBalanced(TreeNode* root) {
if (!root) return true;
int left = height(root->left);
int right = height(root->right);
if (abs(left - right) > 1) return false;
return isBalanced(root->left) && isBalanced(root->right);
}
int height(TreeNode* root) {
if (root == nullptr) {
return 0;
}
return 1 + max(height(root->left), height(root->right));
}
};
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) return true;
int left = height(root.left);
int right = height(root.right);
if (Math.abs(left - right) > 1) return false;
return isBalanced(root.left) && isBalanced(root.right);
}
public int height(TreeNode root) {
if (root == null) {
return 0;
}
return 1 + Math.max(height(root.left), height(root.right));
}
}
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
left = self.height(root.left)
right = self.height(root.right)
if abs(left - right) > 1:
return False
return self.isBalanced(root.left) and self.isBalanced(root.right)
def height(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
return 1 + max(self.height(root.left), self.height(root.right))
/**
* Definition for a binary tree node.
* class TreeNode {
* constructor(val = 0, left = null, right = null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* @param {TreeNode} root
* @return {boolean}
*/
isBalanced(root) {
if (root === null) return true;
let left = this.height(root.left);
let right = this.height(root.right);
if (Math.abs(left - right) > 1) return false;
return this.isBalanced(root.left) && this.isBalanced(root.right);
}
/**
* @param {TreeNode} root
* @return {number}
*/
height(root) {
if (root === null) {
return 0;
}
return (
1 + Math.max(this.height(root.left), this.height(root.right))
);
}
}
2. Depth First Search Method
This method uses recursion to calculate the height of each subtree while checking for balance at the same time. If any subtree is unbalanced, we stop further checks. It’s more efficient since we calculate height and balance in one pass.
- Time complexity: O(n)
- Space complexity: O(h)
- Best Case (balanced tree): O(log(n))
- Worst Case (degenerate tree): O(n)
where n is the number of nodes in the tree and h is the height of the tree.
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isBalanced(TreeNode* root) {
return dfs(root)[0] == 1;
}
private:
vector<int> dfs(TreeNode* root) {
if (!root) {
return {1, 0};
}
vector<int> left = dfs(root->left);
vector<int> right = dfs(root->right);
bool balanced = (left[0] == 1 && right[0] == 1) &&
(abs(left[1] - right[1]) <= 1);
int height = 1 + max(left[1], right[1]);
return {balanced ? 1 : 0, height};
}
};
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
return dfs(root)[0] == 1;
}
private int[] dfs(TreeNode root) {
if (root == null) {
return new int[]{1, 0};
}
int[] left = dfs(root.left);
int[] right = dfs(root.right);
boolean balanced = (left[0] == 1 && right[0] == 1) &&
(Math.abs(left[1] - right[1]) <= 1);
int height = 1 + Math.max(left[1], right[1]);
return new int[]{balanced ? 1 : 0, height};
}
}
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def dfs(root):
if not root:
return [True, 0]
left, right = dfs(root.left), dfs(root.right)
balanced = left[0] and right[0] and abs(left[1] - right[1]) <= 1
return [balanced, 1 + max(left[1], right[1])]
return dfs(root)[0]
/**
* Definition for a binary tree node.
* class TreeNode {
* constructor(val = 0, left = null, right = null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* @param {TreeNode} root
* @return {boolean}
*/
isBalanced(root) {
return this.dfs(root)[0] === 1;
}
/**
* @param {TreeNode} root
* @return {number[]}
*/
dfs(root) {
if (!root) {
return [1, 0];
}
const left = this.dfs(root.left);
const right = this.dfs(root.right);
const balanced =
left[0] === 1 &&
right[0] === 1 &&
Math.abs(left[1] - right[1]) <= 1;
const height = 1 + Math.max(left[1], right[1]);
return [balanced ? 1 : 0, height];
}
}
3. Depth First Search(Stack) Method
Instead of recursion, this approach uses a stack to manually traverse the tree like DFS. It keeps track of subtree heights and balance as we go. This avoids recursion but can be a bit more complex to implement.
- Time complexity: O(n)
- Space complexity: O(n)
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isBalanced(TreeNode* root) {
stack<TreeNode*> stack;
TreeNode* node = root;
TreeNode* last = nullptr;
unordered_map<TreeNode*, int> depths;
while (!stack.empty() || node != nullptr) {
if (node != nullptr) {
stack.push(node);
node = node->left;
} else {
node = stack.top();
if (node->right == nullptr || last == node->right) {
stack.pop();
int left = depths[node->left];
int right = depths[node->right];
if (abs(left - right) > 1) return false;
depths[node] = 1 + max(left, right);
last = node;
node = nullptr;
} else {
node = node->right;
}
}
}
return true;
}
};
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class Solution {
public boolean isBalanced(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
TreeNode node = root, last = null;
Map<TreeNode, Integer> depths = new HashMap<>();
while (!stack.isEmpty() || node != null) {
if (node != null) {
stack.push(node);
node = node.left;
} else {
node = stack.peek();
if (node.right == null || last == node.right) {
stack.pop();
int left = depths.getOrDefault(node.left, 0);
int right = depths.getOrDefault(node.right, 0);
if (Math.abs(left - right) > 1) return false;
depths.put(node, 1 + Math.max(left, right));
last = node;
node = null;
} else {
node = node.right;
}
}
}
return true;
}
}
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root):
stack = []
node = root
last = None
depths = {}
while stack or node:
if node:
stack.append(node)
node = node.left
else:
node = stack[-1]
if not node.right or last == node.right:
stack.pop()
left = depths.get(node.left, 0)
right = depths.get(node.right, 0)
if abs(left - right) > 1:
return False
depths[node] = 1 + max(left, right)
last = node
node = None
else:
node = node.right
return True
/**
* Definition for a binary tree node.
* class TreeNode {
* constructor(val = 0, left = null, right = null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* @param {TreeNode} root
* @return {boolean}
*/
isBalanced(root) {
let stack = [];
let node = root, last = null;
let depths = new Map();
while (stack.length > 0 || node !== null) {
if (node !== null) {
stack.push(node);
node = node.left;
} else {
node = stack[stack.length - 1];
if (node.right === null || last === node.right) {
stack.pop();
let left = depths.get(node.left) || 0;
let right = depths.get(node.right) || 0;
if (Math.abs(left - right) > 1) return false;
depths.set(node, 1 + Math.max(left, right));
last = node;
node = null;
} else {
node = node.right;
}
}
}
return true;
}
}


