Insertion Sort in C++

July 9, 2025

What is Insertion Sort in C++?

Rearranging data in a logical order is known as sorting i.e. arranging of data in ascending or descending order. In this article, we will learn about insertion sort in C++.

Insertion sorting is done in the same way as we sort our cards in while we play games of cards

Time Complexity	O(n²)
Best Case	Ω(n)
Worst Case	O(n²)
Aux. Space Complexity	O(1)
Best case when	Array is already sorted
Worst case when	Array is reverse sorted

What is Insertion Sort in C++?

Rearranging data in a logical order is known as sorting i.e. arranging of data in ascending or descending order. In this article, we will learn about insertion sort in C++.

Insertion sorting is done in the same way as we sort our cards in while we play games of cards

Time Complexity	O(n²)
Best Case	Ω(n)
Worst Case	O(n²)
Aux. Space Complexity	O(1)
Best case when	Array is already sorted
Worst case when	Array is reverse sorted

Insertion Sort in C++

If there are n element and it requires (n-1) pass to sort them then, at each pass we insert current element in the appropriate position so that the element are in order. Some characteristics of insertion sort in C++.

A sub-list is maintained which is always in sorted order.
It is better then Selection Sort and Bubble Sort algorithms.
It is efficient for smaller data sets but inefficient for larger data sets.
Its space complexity is less.
It does not change the relative order of elements which are equal.

Prime Course Trailer

Related Banners

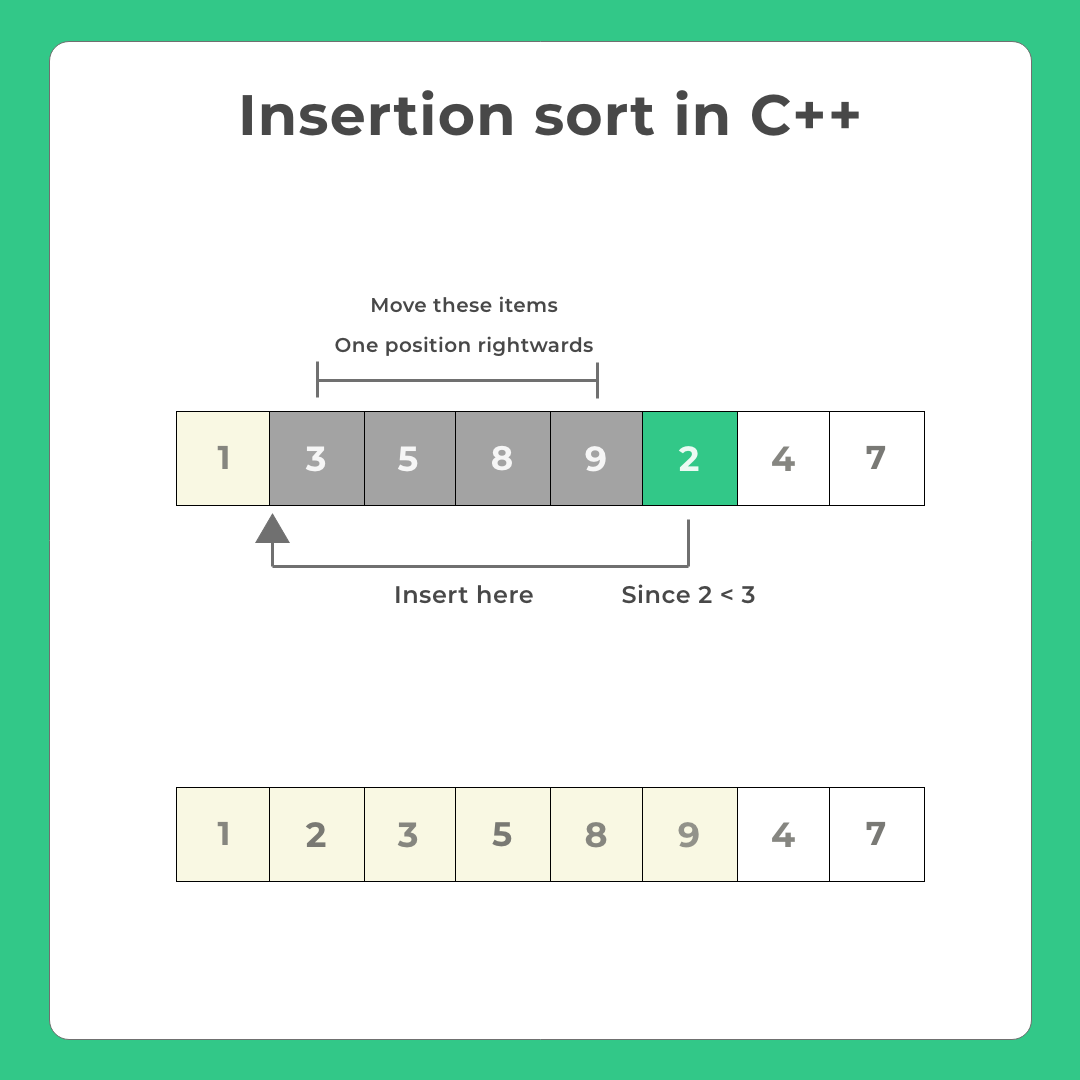
Execution of insertion sort in C++

It’s almost similar to how we play cards.
At any given time, one part of the array will be sorted and one part will be unsorted.
We will pick the leftmost item from the unsorted part
Insert this item at the correct position in the sorted array

You can check the implementation of the same below

Algorithm for insertion sort in C++

INSERTION-SORT(A)
for i = 1 to n
key ← A [i]
j ← i – 1
while j > = 0 and A[j] > key
A[j+1] ← A[j]
j ← j – 1
End while
A[j+1] ← key
End for

Program for insertion sort in C++

Run

// C++ Program for Insertion Sort
// Time Complexity : O(N^2)
// Space Compelexity : O(1)
// Best Case : When already Sorted, Worst Case : When reverse Sorted
#include<iostream>
using namespace std;

//Function to print array.
void display(int arr[], int size) 
{ 
    int i; 
    for (i = 0; i < size; i++) 
    cout << arr[i] << "\t"; 
    cout << "\n"; 
} 

//Main function to run the program.
int main() 
{ 
    int array[] = {5, 3, 1, 9, 8, 2, 4,7}; 
    int size = sizeof(array)/sizeof(array[0]); 

    cout << "Before Insertion sort: \n";
    display(array, size);

    int i, key, j;  
    for (i = 1; i < size; i++) { key = array[i]; j = i - 1; /* Here the elements in b/w arrary[i-1 & 0] which are greater than key are moved ahead by 1 position each*/ while (j >= 0 && array[j] > key) 
        {  
            array[j + 1] = array[j];  
            j = j - 1;  // moving backwards
        }
        // placing key item now
        array[j + 1] = key;  
    }
    cout << "After Insertion sort: \n"; 
    display(array, size);
    
    return 0; 
}

Output

Before Insertion sort:
5  3  1  9  8  2  4  7
After Insertion sort: 
1  2  3  4  5  7  8  9

Pros and Cons of Insertion Sort Algorithm

Pros

Anyone can write it is moderately easy to understand
Only O(1) space requirements
For a smaller number of items in an array it’s quicker than merge sort

Cons

Not so good average time complexity of O(n²)
If there are large elements then it gives bad performance because of O(n^2) time complexity
Shifting items because of insertion can be costly

Other information

Best Case: If already sorted data set
Worst Case: Sorted data set but in the opposite order

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Sorting

Sorting algorithms are easy to learn but are really important for college semester exams and companies offering package between 3 – 6 LPA would ask direct searching questions in online test/ interviews.

Classification of Sorting Algorithms
Bubble Sort – C | C++ | Java
Insertion Sort – C | C++ | Java
Selection Sort – C | C++ | Java
Merge Sort – C | C++ | Java
Quick Sort – C | C++ | Java
Counting Sort – C | C++ | Java
Radix Sort – C | C++ | Java
Heap Sort – C | C++ | Java

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Checkout list of all the video courses in PrepInsta Prime Subscription

Insertion Sort in C

September 18, 2025

How Insertion Sort works in C

In this technique, we pick an Element and then insert it at the appropriate position in ascending and descending order.

The inspiration has been taken from playing cards

Time Complexity	O(n²)
Best Case	Ω(n)
Worst Case	O(n²)
Aux. Space Complexity	O(1)
Best case when	Array is already sorted
Worst case when	Array is reverse sorted

Insertion Sort in C

Insertion sort is just like how to sort playing cards in your hands. You pick one card and try to place that card in its correct position.

The array is kind of split into a sorted part and an unsorted part. A value from the unsorted part is picked and placed into its correct position in the sorted part.

Below are examples on how you can do the same.

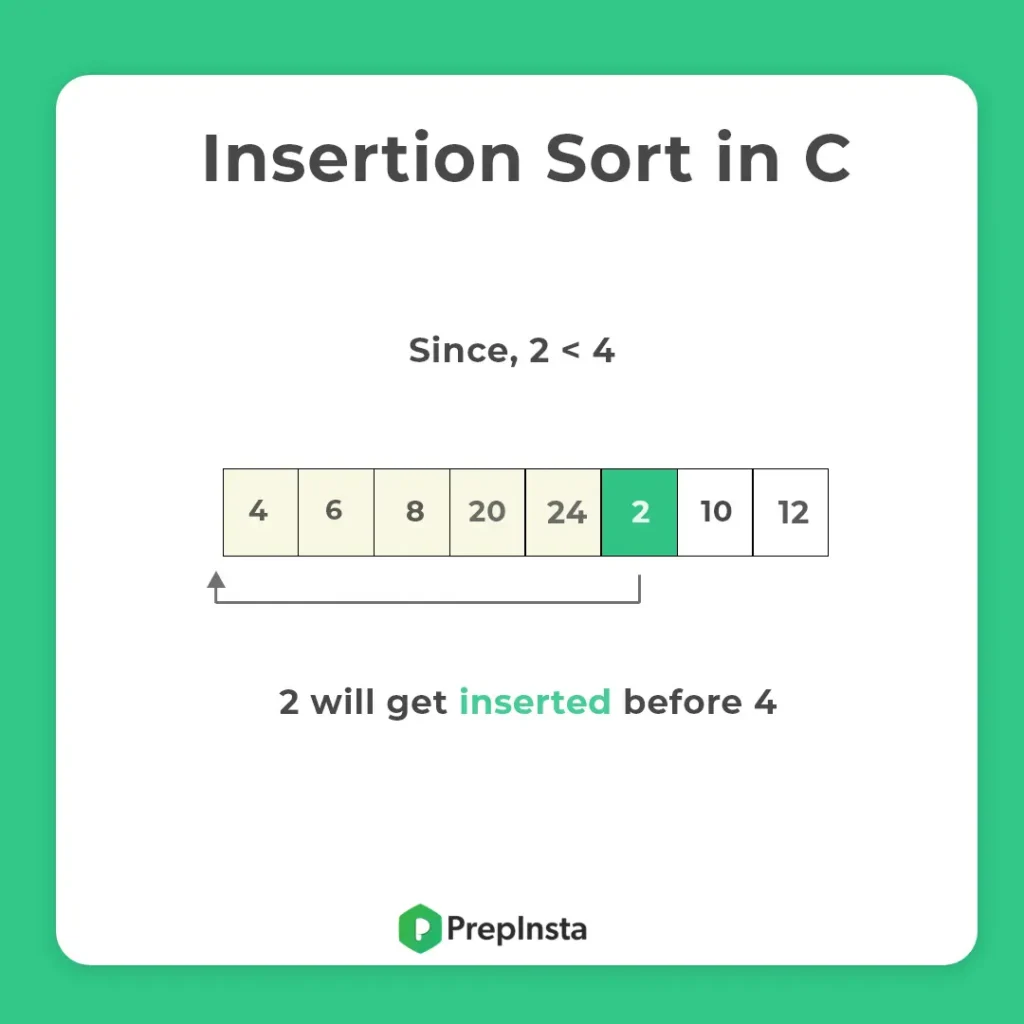
Execution of Insertion Sort in C

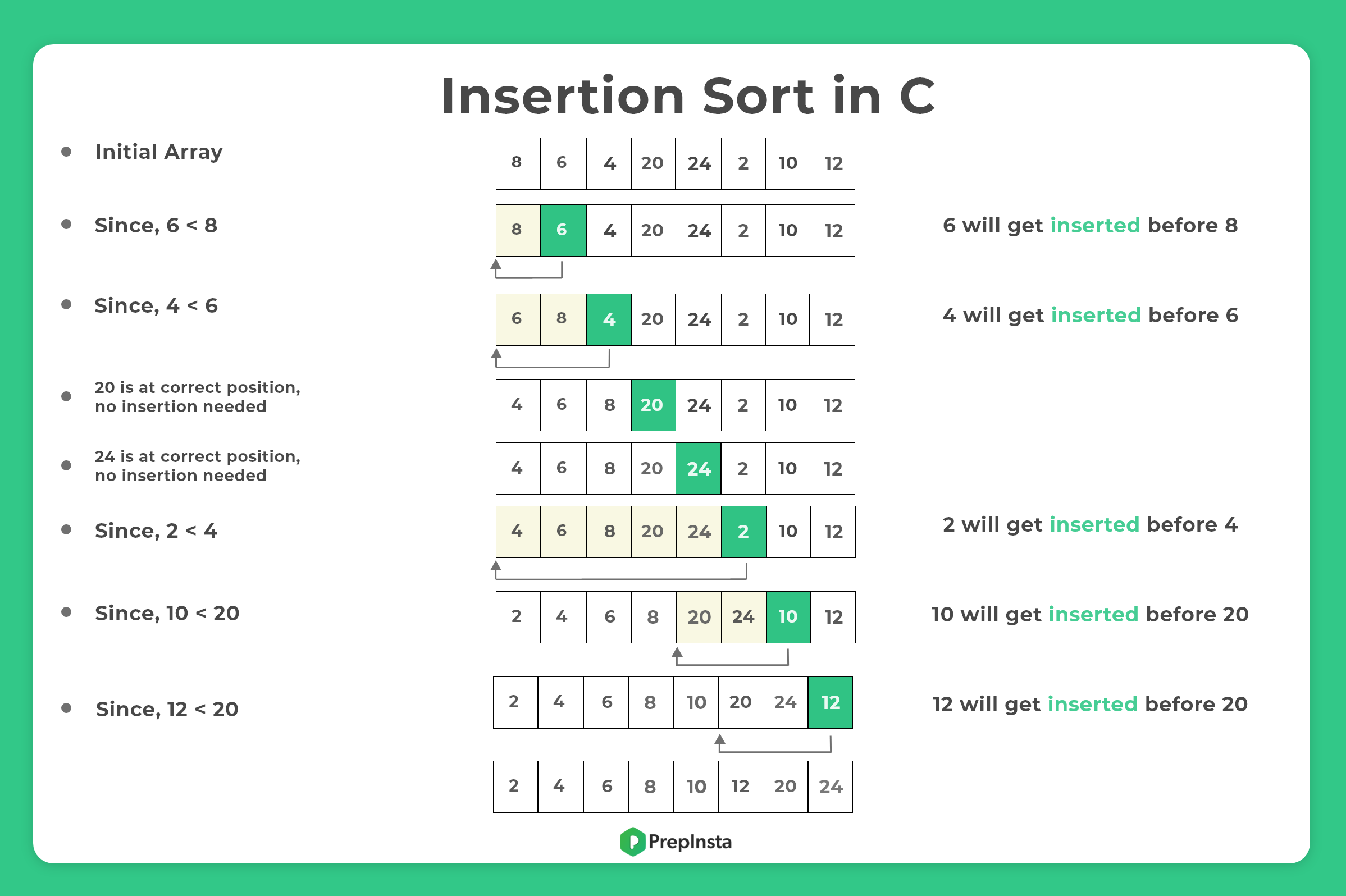
Approach of Insertion Sort

Iterate over the whole array, picking each item in the array once iteratively
Call this picked item key
If this key item is smaller than its predecessor, compare it to the item before
To make space for this swapped item move items greater than key one position right
Keep doing this until you find a smaller element than key element.

Code of Insertion Sort

Normal

Using Driver function

Normal

Run

#include<stdio.h>

// Function to print array 
void display(int arr[], int size) 
{ 
    int i; 
    for (i = 0; i < size; i++) 
        printf("%d ", arr[i]); 
    printf("\n"); 
} 

// Main function to run the program
int main() 
{ 
    int array[] = {8, 6, 4, 20, 24, 2, 10, 12}; 
    int size = sizeof(array)/sizeof(array[0]); 

    printf("Before Insertion sort: \n");
    display(array, size);

    int i, key, j;  
    for (i = 1; i < size; i++) 
    {
        key = array[i]; 
        j = i - 1; 

        /* Here the elements in b/w array[0 to i-1] 
        which are greater than key are moved ahead 
        by 1 position each*/ 
        while (j >= 0 && array[j] > key) 
        {  
            array[j + 1] = array[j];  
            j = j - 1;  
        }
        // placing element at its correct position
        array[j + 1] = key;  
    }
    
    printf("After Insertion sort: \n"); 
    display(array, size); 
    
    return 0; 
}
// Time Complexity : O(n^2)
// Auxiliary Space : O(1)

Output:

Before Insertion sort: 
8 6 4 20 24 2 10 12 
After Insertion sort: 
2 4 6 8 10 12 20 24

Using Driver function

Run

#include<stdio.h>

// Here we are implementing Insertion sort
void insertionSort(int array[], int size) 
{ 
    int i, key, j; 
    for (i = 1; i < size; i++) 
    { 
        key = array[i]; 
        j = i - 1; 

        /* Here the elements in b/w array[0 to i-1]
        which are greater than key are moved ahead 
        by 1 position each*/ 
        while (j >= 0 && array[j] > key) 
        { 
            array[j + 1] = array[j]; 
            j = j - 1; 
        } 
        array[j + 1] = key; 
    }
} 

/* Function to print array */
void display(int arr[], int size) 
{ 
    int i; 
    for (i=0; i < size; i++) 
        printf("%d ", arr[i]); 
    printf("\n"); 
} 

// Main function to run the program
int main() 
{ 
    int array[] = {5, 3, 1, 9, 8, 2, 4, 7}; 
    int size = sizeof(array)/sizeof(array[0]); 

    printf("Before Insertion sort: \n");
    display(array, size); 

    insertionSort(array, size);

    printf("After Insertion sort: \n"); 
    display(array, size); 
    return 0; 
}
// Time Complexity : O(n^2) 
// Auxiliary Space : O(1)

Output:

Before Insertion sort:
5 3 1 9 8 2 4 7 
After Insertion sort: 
1 2 3 4 5 7 8 9

Some facts about Insertion sort

Time Complexity: O(n²)
Auxiliary Space: O(1)
Best Case: Ω(n), when the array is already sorted
Worst Case: Θ(n^2), when the array is reverse sorted.
Algorithmic Paradigm: Incremental Approach
Sorting In Place: Yes
Stable: Yes

Advantages and Disadvantages of Insertion Sort

Advantages

It is simple, small and easy to write.
It doesn’t use a lot of overhead.
It uses in place sorting, thus O(1) space requirements
If data is almost sorted, then it can be very fast approaching O(n) and faster than Merge sort(for sorted data, and small N, else merge sort is faster)
Efficient for (quite) small data sets.

Disadvantages

Poor average time complexity of O(n²)
If there are a large number of elements then it is inefficient
Many items needs to be shifted to one insertion

Properties

You will encounter the best case if the data is already or nearly sorted
It will give worst-case results if the array is sorted in the opposite order as required

Time Complexity
For Linear Search

Best

Ω(n)

Average

O(n²)

Worst

Θ(n²)

Space Complexity

O(1)

Time Complexity
For Linear Search

Best

O(n)

Average

O(n²)

Worst

Θ(n²)

Space Complexity

O(1)

Quiz Time

Question 1. How many passes does an insertion sort algorithm consist of? –

(Flipkart – HackerEarth Test)

Solution & Explanation

Explanation: An insertion algorithm consists of N-1 passes when an array of N elements is given.

Question 2. For the following question, how will the array elements look like after second pass?

35, 7, 64, 57, 28, 14

8, 21, 32, 34, 51, 64
8, 32, 34, 51, 64, 21
8, 34, 51, 64, 32, 21
8, 34, 64, 51, 32, 21

(TCS NQT)

Solution & Explanation

Original Array :

35, 7, 64, 57, 28, 14

After Pass 1 : 7, 35, 64, 57, 28, 14

After Pass 2 : 7, 35, 64, 57, 28, 14 (no change)

After Pass 3 : 7, 35, 57, 64, 28, 21 (no swapping)

After Pass 4 : 7, 28, 35, 57, 64, 14 (no swapping)

Sorting

Classification of Sorting Algorithms
Bubble Sort – C | C++ | Java
Insertion Sort – C | C++ | Java
Selection Sort – C | C++ | Java
Merge Sort – C | C++ | Java
Quick Sort – C | C++ | Java
Counting Sort – C | C++ | Java
Radix Sort – C | C++ | Java
Heap Sort – C | C++

Unlock this article for Free, by logging in

Insertion Sort in C++

What is Insertion Sort in C++?

What is Insertion Sort in C++?

Insertion Sort in C++

Prime Course Trailer

Related Banners

Execution of insertion sort in C++

Algorithm for insertion sort in C++

Program for insertion sort in C++

Output

Pros and Cons of Insertion Sort Algorithm

Pros

Cons

Other information

Sorting

Get over 200+ course One Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Insertion Sort in C

How Insertion Sort works in C

Insertion Sort in C

Execution of Insertion Sort in C

Approach of Insertion Sort

Code of Insertion Sort

Output:

Output:

Some facts about Insertion sort

Advantages and Disadvantages of Insertion Sort

Advantages

Disadvantages

Properties

Time Complexity For Linear Search

Best

Average

Worst

Space Complexity

Time Complexity For Linear Search

Best

Average

Worst

Space Complexity

Quiz Time

Sorting

Unlock this article for Free,
by logging in

Time Complexity
For Linear Search

Time Complexity
For Linear Search