0
Notifications Mark All Read
- Login
- Get Prime
Preorder Tree Traversal without recursion in Java
Preorder Traversal Without recursion
In preorder traversal , root is visited first , then the left subtree and at last right subtree. Preorder traversal is also used to get an prefix expression of an expression. We need one explicit stack to implement this traversal without recursion.
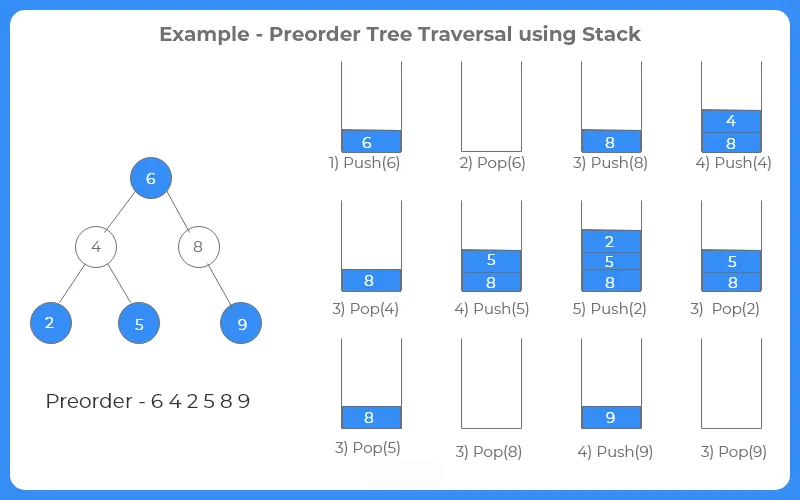
Steps to find preorder traversal using stack:
- Step 1: Create an empty stack and put the root element into it. i.e Stack-> 6.
- Step 2: Now check if the stack is non- empty. if so , then pop an element from the stack i.e. 6 and print it.
- Step 3: Now check if right child of popped element is not null. If so, then push the element into stack . So stack become , Stack->8.
- Step 4: Similarly check for left child . If so , then push the left child into stack . So stack become , Stack->4,8 .And again goto step 3 and check if stack is not null.
- Step 5: Again pop the top element from stack and print it. i.e print 4.
- Step 6: Check if the right child is not null . If so , then push the right child into stack. i.e push(5) . So stack become , Stack->5,8.
- Step 7: Similarly , check for left child. If it is not null , then push it into stack. i.e. push(2). So our stack become Stack->2,5,8. and again goto step 3 and check if stack is not null.
- Step 8: Again pop an element from the stack and print it. i.e. print 2.Now stack become Stack->5,8.
- Step 9: Now , it’s left and right child is not available hence we again goto step 3.
- Step 10: pop an element from the stack i.e. pop(5) and print it.
- Step 11: Now , As it’s left and right child is not available so move to step 3.
- Step 12: pop an element from the stack i.e. 8 and print it.
- Step 13: Now, check for it’s right child as 9 is it’s right child so put it into the stack. and goto step 3 as there is no left child of element 8.
- Step 14: pop the element from the stack i.e. 9 and print it . Now our stack becomes empty, so stop.
Therefore the sequence will be printed as 6,4,2,5,8,9
Algorithm to find Preorder traversal of binary tree using stack
- If root is null , simply return.
- else , create an empty stack and push root node into it.
- Check if the Stack is non-empty . If so, pop the element from the stack and print it.
- Now, Check if the right child of popped element is available or not . if available then push it into stack.
- Similarly , Check for the left child . If available then push it into the stack.
- Now , continue step 3 ,4,5 until stack becomes empty .
- If Stack becomes empty then stop.
Run
//Preorder Traversal Without recursion
/*Node class containing left and right child of current node and key value.*/
import java.util.*;
class Node{
int value;
Node left,right;
public Node(int value)
{
this.value=value;
left=null;
right=null;
}
}
class Preorder{
Node root; //root of the tree
public Preorder(){
root=null;
}
/*function for Preorder traversal of the binary tree*/
public void preorder()
{
if(root ==null)
return ;
Stack stack=new Stack(); //creating an empty stack.
stack.push(root); //inserting an element into stack.
while(!stack.isEmpty())
{
Node temp=(Node)stack.pop(); //removing the top element from stack.
System.out.print(temp.value+" ");
if(temp.right!=null)
stack.push(temp.right); //inserting into stack
if(temp.left!=null)
stack.push(temp.left); //inserting into stack
}
}
}
public class Main{
public static void main(String[] args)
{
Preorder t=new Preorder();
t.root=new Node(6);
t.root.left=new Node(4);
t.root.right=new Node(8);
t.root.left.left=new Node(2);
t.root.left.right=new Node(5);
t.root.right.right=new Node(9);
t.preorder();
}
}
Output :
6 4 2 5 8 9
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java

 0
0


