Quick Sort in C++

June 4, 2022

How Quick Sort works in C++

In the process of sorting we arrange the given data in either ascending or descending order this means that we try to arrange the data in a logical form.

Quick sort  is an algorithm of the divide and conquer type

quickly
Time Complexity O(n log n)
Best Case O(n log n)
Worst Case O(n2)
Space Complexity O(1)
Auxiliary Space Complexity O(log n)
In Place Yes
Stable No

How it works?

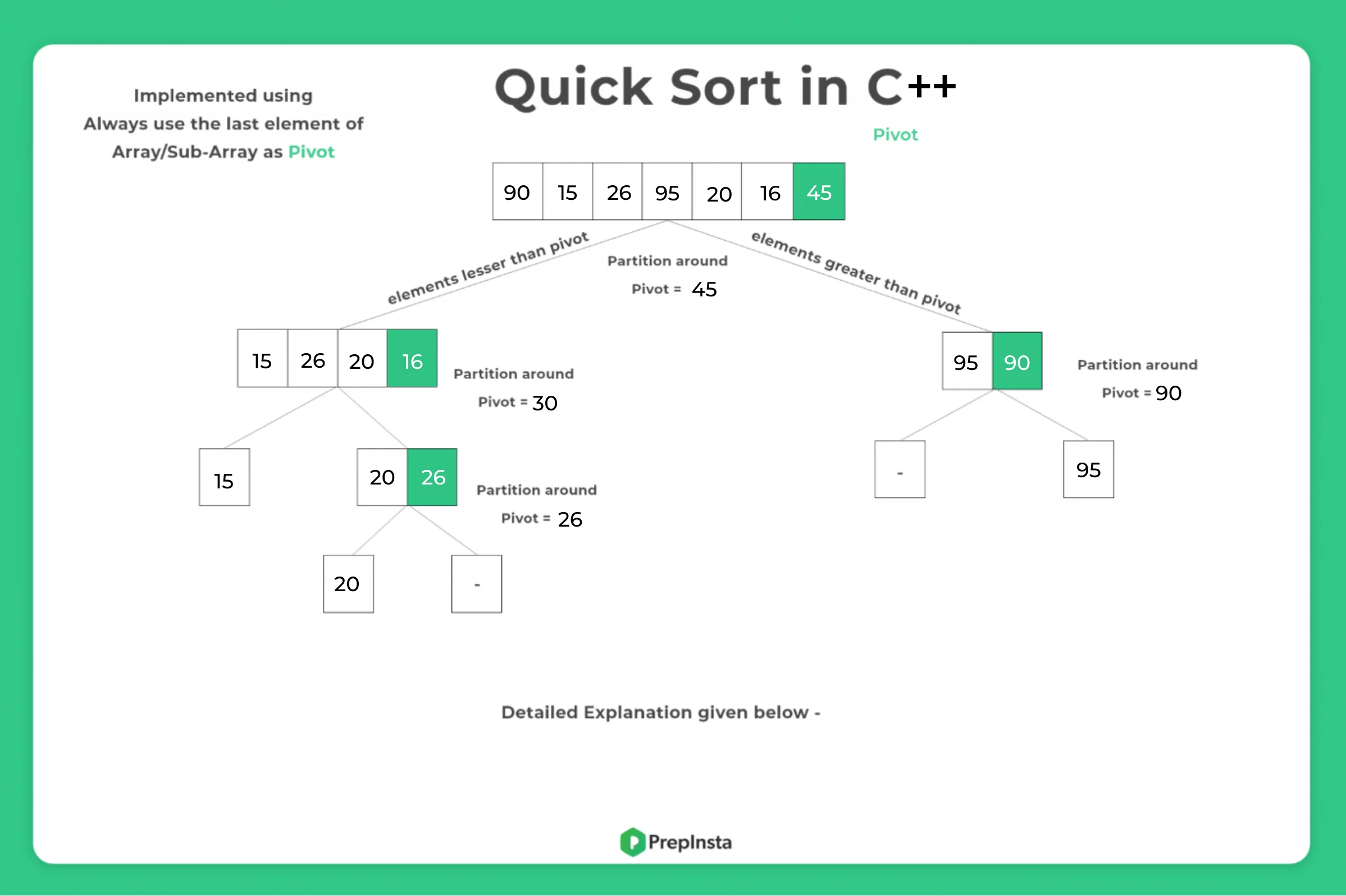
Quick sort works in the following way – 

  • Choose an item from array called as pivot
  • Move all the elements smaller than pivot to left partition
  • Move all the elements greater than pivot to right partition.

Choose new pivot item in each partition and keep doing the same process again until partition of one element each aren’t formed.

How to choose a pivot element for quick sort in C++?

Pivot can be selected in the following ways:-

  • First element as the pivot.
  • Last element as pivot
  • Random element as pivot.
  • Median element as pivot.

We will be choosing the last element as pivot.

Quick Sort in C++
Quick Sort in C++ 2
Run
#include<iostream>
using namespace std;
  
//Function to swap two elements. 
void swap(int* x, int* y) 
{ 
    int temp = *x; 
    *x = *y; 
    *y = temp; 
} 
  
/* Partition function to do Partition
elements on the left side of pivot elements would be smaller than pivot
elements on the right side of pivot would be greater than the pivot
*/
int partition (int array[], int low, int high) 
{ 
    //Pivot element selected as right most element in array each time.
    int pivot = array[high];    
    int swapIndex  = (low - 1);   //swapping index.
  
    for (int j = low; j <= high- 1; j++) 
    { 
        //Check if current element is smaller than pivot element.
        if (array[j] < pivot) 
        { 
            swapIndex ++;    //increment swapping index.
            swap(&array[swapIndex], &array[j]); 
        } 
    } 
    swap(&array[swapIndex + 1], &array[high]); 
    return (swapIndex + 1); 
} 
  
//Recursive function to apply quickSort
void quickSort(int array[], int low, int high) 
{ 
    if (low < high) 
    { 
       /* indexPI is partitioning index, partition() function will 
        return index of partition */
        int indexPI  = partition(array, low, high); 
  
        quickSort(array, low, indexPI  - 1);  //left partition
        quickSort(array, indexPI  + 1, high); //right partition
    } 
} 
  
//Function to display the array
void display(int array[], int size) 
{ 
    int i; 
    for (i=0; i < size; i++) 
        cout<< array[i] <<" "; 
} 
  
//Main function to run the program
int main() 
{ 
    int array[] = {7, 9, 1, 3, 5, 2, 6, 0, 4, 8}; 
    int size = sizeof(array)/sizeof(array[0]);
    
    cout<<"Before Sorting: \n";
    display(array, size);
    
    quickSort(array, 0, size-1); 
    
    cout<<"\nAfter Sorting: \n"; 
    display(array, size); 
    
    return 0; 
}

Output

Before Sorting: 
7 9 1 3 5 2 6 0 4 8 

After Sorting: 
0 1 2 3 4 5 6 7 8 9

Facts about Quick Sort

Time Complexity

  • Best Case – O(n log n)
  • Avg Case – O(n log n)
  • Worst Case – O(n log n)

The best-case occurs when the partitions are as evenly balanced as possible. Basically, partition sizes on either side of the pivot are as even as possible. Using the height of the tree (Log2(N+1) – 1) we can calculate time complexity.

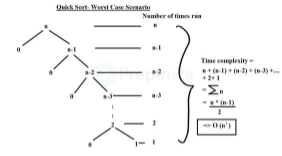
The worst case would occur when the array arrangement is such that it is most unbalanced as possible and is just growing on one side of the pivot. (check image)

Quick Sort best case

Space Complexity

The space complexity is O(1) since we do not use any other external array to do sorting and neither space requirements grow with array size.

However, the auxiliary space complexity is O(log n) due to the function call stack.

The worst-case space complexity will be O(n) which is in the case when array arrangement leads to the partition being highly unbalanced and is just growing on one side of the pivot.

Other Facts

  • Quicksort is an in-place algorithm. In-place sorting means, it does not use additional storage space to perform sorting.
  • The algorithm is efficient for large-sized data sets.
  • The average or best-case complexity of quicksort is O(n log n).
  • The quicksort is an in-place, divide-and-conquer, massively recursive sort algorithm.
  • The worst-case efficiency of the quicksort is o(n²) when the list is sorted and the leftmost element is chosen as the pivot.
Quick sort in C meme

Sorting

Sorting algorithms are easy to learn but are really important for college semester exams and companies offering package between 3 – 6 LPA would ask direct searching questions in online test/ interviews.

Data Structures and Algorithm Learn Sorting